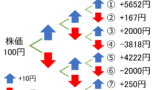
投資のリスク軽減方法の一つとして「時間分散」があります。ドルコスト平均法とも呼ばれています。
積立投資により実現されるこの手法に対して、株価がどのような動きのときにどのような損益が生じるのでしょうか。この記事では実際にシミュレーションを通じて積立投資による時間分散効果についての損益を図説します。どういった場面で利益が上がりやすか理解できると思いますので、参考にしていただければと思います。
なお、単純な値動きに対する一括購入の場合とつみたてによる違いは以下の記事で解説しています。
今回は上の記事とは少し違った視点で、つみたてによる効果と運用の損益について見ていきたいと思います。
時間分散「つみたて」による効果
このシミュレーションでは、最初の株価を1株100円程度とし、プラスマイナス20円以内の変動後に最後に最初の株価に戻る動きを想定し、その値動きの中で毎月1万円ずつ3年間積立をします。つまり、投資金額は合計で36万円となり、一括で購入して最後に一括で売却した場合は損益は0になります。
今回、4パターンの値動きを想定し、積立の効果によって最終的にどのような損益が生じるのか、また、つみたて期間中はどのような損益が生じているのかについて考察します。
値動きパターン1:上下
下図のように、上がった後に下がり、最後にまた戻るサインカーブのような値動きの場合を想定します。
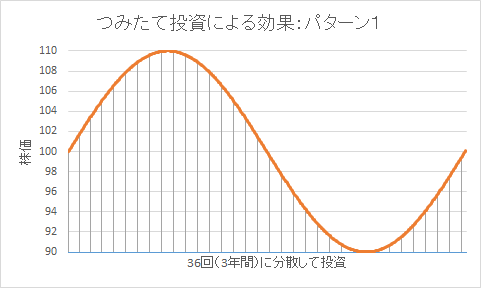
36回のそれぞれの購入時の株価とそれに応じた購入株数などをまとめると以下の表になります。
| 購入 回数 | 株価 | 10,000円で 買える株数 | 投資額 | 評価額 | 損益 |
| 1 | 100.0 | 100.0 | 10,000 | 10,000 | 0 |
| 2 | 101.8 | 98.3 | 20,000 | 20,178 | 178 |
| 3 | 103.5 | 96.6 | 30,000 | 30,520 | 520 |
| 4 | 105.1 | 95.1 | 40,000 | 40,995 | 995 |
| 5 | 106.6 | 93.8 | 50,000 | 51,560 | 1,560 |
| 6 | 107.8 | 92.8 | 60,000 | 62,159 | 2,159 |
| 7 | 108.8 | 91.9 | 70,000 | 72,729 | 2,729 |
| 8 | 109.5 | 91.3 | 80,000 | 83,203 | 3,203 |
| 9 | 109.9 | 91.0 | 90,000 | 93,510 | 3,510 |
| 10 | 110.0 | 90.9 | 100,000 | 103,585 | 3,585 |
| 11 | 109.8 | 91.1 | 110,000 | 113,367 | 3,367 |
| 12 | 109.2 | 91.6 | 120,000 | 122,806 | 2,806 |
| 13 | 108.4 | 92.3 | 130,000 | 131,864 | 1,864 |
| 14 | 107.3 | 93.2 | 140,000 | 140,519 | 519 |
| 15 | 105.9 | 94.4 | 150,000 | 148,767 | ▲ 1,233 |
| 16 | 104.4 | 95.8 | 160,000 | 156,622 | ▲ 3,378 |
| 17 | 102.7 | 97.3 | 170,000 | 164,119 | ▲ 5,881 |
| 18 | 101.0 | 99.0 | 180,000 | 171,313 | ▲ 8,687 |
| 19 | 99.2 | 100.8 | 190,000 | 178,281 | ▲ 11,719 |
| 20 | 97.4 | 102.6 | 200,000 | 185,115 | ▲ 14,885 |
| 21 | 95.8 | 104.4 | 210,000 | 191,923 | ▲ 18,077 |
| 22 | 94.2 | 106.1 | 220,000 | 198,828 | ▲ 21,172 |
| 23 | 92.9 | 107.7 | 230,000 | 205,959 | ▲ 24,041 |
| 24 | 91.7 | 109.0 | 240,000 | 213,451 | ▲ 26,549 |
| 25 | 90.9 | 110.1 | 250,000 | 221,435 | ▲ 28,565 |
| 26 | 90.3 | 110.8 | 260,000 | 230,036 | ▲ 29,964 |
| 27 | 90.0 | 111.1 | 270,000 | 239,365 | ▲ 30,635 |
| 28 | 90.1 | 111.0 | 280,000 | 249,513 | ▲ 30,487 |
| 29 | 90.4 | 110.6 | 290,000 | 260,545 | ▲ 29,455 |
| 30 | 91.1 | 109.7 | 300,000 | 272,499 | ▲ 27,501 |
| 31 | 92.1 | 108.6 | 310,000 | 285,375 | ▲ 24,625 |
| 32 | 93.3 | 107.2 | 320,000 | 299,140 | ▲ 20,860 |
| 33 | 94.7 | 105.6 | 330,000 | 313,721 | ▲ 16,279 |
| 34 | 96.3 | 103.8 | 340,000 | 329,010 | ▲ 10,990 |
| 35 | 98.0 | 102.0 | 350,000 | 344,867 | ▲ 5,133 |
| 36 | 99.8 | 100.2 | 360,000 | 361,119 | 1,119 |
| 最終値 | 100.0 | 360,000 | 361,776 | 1,776 |
最初の上昇局面では利益が出ていますが、その後ピークを過ぎて少し落ちると損失が生じはじめています。なんとか最後は利益がプラスになっていますが、投資額36万円に対して約0.5%です。計算時の四捨五入などの誤差もあるため、最後のプラスはほどんどないものと考えて良いでしょう。
積立時の損益を値動きのグラフに反映させると以下の図のようになります。
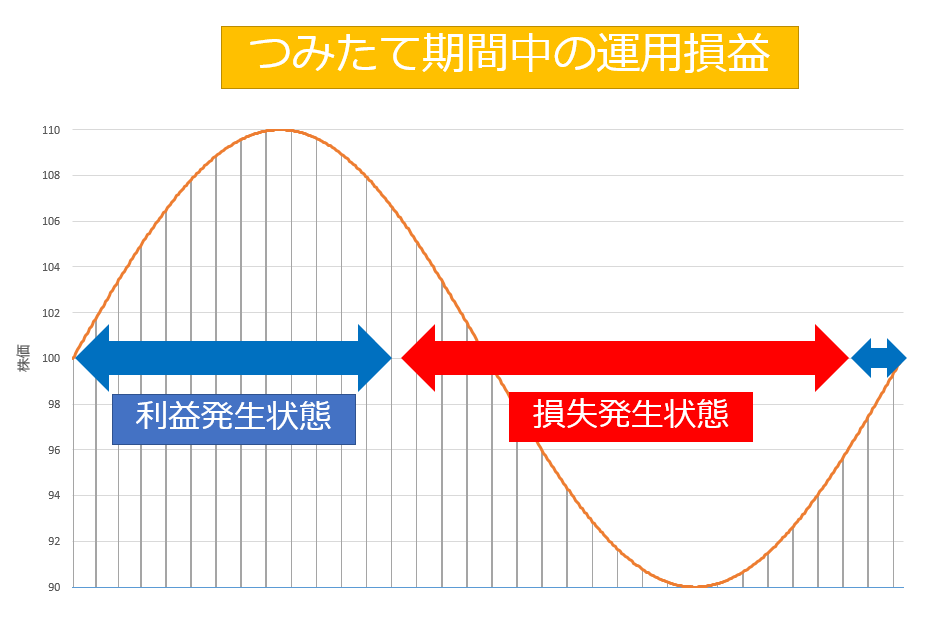
積立期間において運用状況がプラスの期間よりもマイナスの方が長いので、実際のところ、投資している人の気持ち的にはつらいでしょう。下がり続ける局面で、元の株価まで戻ると信じて耐え続けるメンタルが大事になるところだと思います。
一般に言われている「積立は株価が下がっているときこそ、多くの株数が買えるから良い」ということはわかっていても、損失が大きくなるのを見てしまうと、不安が拭えず投資を止めてしまうことがあるかもしれません。しかし、このように株価が最後には元に戻る場合は、そこで投資を止めてしまうことが損失を最も大きくする最悪なシナリオとなります。
値動きパターン2:下上
下図のように、サインカーブの逆位相となるような値動きの場合を想定します。
36回のそれぞれの購入時の株価とそれに応じた購入株数などをまとめると以下の表になります。
| 購入 回数 | 株価 | 10,000円で 買える株数 | 投資額 | 評価額 | 損益 |
| 1 | 100.0 | 100.0 | 10,000 | 10,000 | 0 |
| 2 | 98.2 | 101.8 | 20,000 | 19,822 | ▲ 178 |
| 3 | 96.5 | 103.6 | 30,000 | 29,474 | ▲ 526 |
| 4 | 94.9 | 105.4 | 40,000 | 38,982 | ▲ 1,018 |
| 5 | 93.4 | 107.0 | 50,000 | 48,387 | ▲ 1,613 |
| 6 | 92.2 | 108.5 | 60,000 | 57,746 | ▲ 2,254 |
| 7 | 91.2 | 109.6 | 70,000 | 67,126 | ▲ 2,874 |
| 8 | 90.5 | 110.5 | 80,000 | 76,605 | ▲ 3,395 |
| 9 | 90.1 | 111.0 | 90,000 | 86,263 | ▲ 3,737 |
| 10 | 90.0 | 111.1 | 100,000 | 96,178 | ▲ 3,822 |
| 11 | 90.2 | 110.8 | 110,000 | 106,425 | ▲ 3,575 |
| 12 | 90.8 | 110.2 | 120,000 | 117,066 | ▲ 2,934 |
| 13 | 91.6 | 109.1 | 130,000 | 128,146 | ▲ 1,854 |
| 14 | 92.7 | 107.8 | 140,000 | 139,692 | ▲ 308 |
| 15 | 94.1 | 106.3 | 150,000 | 151,708 | 1,708 |
| 16 | 95.6 | 104.6 | 160,000 | 164,172 | 4,172 |
| 17 | 97.3 | 102.8 | 170,000 | 177,037 | 7,037 |
| 18 | 99.0 | 101.0 | 180,000 | 190,234 | 10,234 |
| 19 | 100.8 | 99.2 | 190,000 | 203,668 | 13,668 |
| 20 | 102.6 | 97.5 | 200,000 | 217,228 | 17,228 |
| 21 | 104.2 | 95.9 | 210,000 | 230,786 | 20,786 |
| 22 | 105.8 | 94.5 | 220,000 | 244,204 | 24,204 |
| 23 | 107.1 | 93.3 | 230,000 | 257,342 | 27,342 |
| 24 | 108.3 | 92.4 | 240,000 | 270,058 | 30,058 |
| 25 | 109.1 | 91.6 | 250,000 | 282,219 | 32,219 |
| 26 | 109.7 | 91.1 | 260,000 | 293,703 | 33,703 |
| 27 | 110.0 | 90.9 | 270,000 | 304,408 | 34,408 |
| 28 | 109.9 | 91.0 | 280,000 | 314,254 | 34,254 |
| 29 | 109.6 | 91.3 | 290,000 | 323,188 | 33,188 |
| 30 | 108.9 | 91.8 | 300,000 | 331,188 | 31,188 |
| 31 | 107.9 | 92.7 | 310,000 | 338,262 | 28,262 |
| 32 | 106.7 | 93.7 | 320,000 | 344,454 | 24,454 |
| 33 | 105.3 | 95.0 | 330,000 | 349,842 | 19,842 |
| 34 | 103.7 | 96.5 | 340,000 | 354,534 | 14,534 |
| 35 | 102.0 | 98.1 | 350,000 | 358,670 | 8,670 |
| 36 | 100.2 | 99.8 | 360,000 | 362,418 | 2,418 |
| 最終値 | 100.0 | 360,000 | 362,418 | 1,760 |
最初の下落局面で損失が出ていますが、その後回復してくると利益が出はじめています。パターン1と同様に最終的には投資額36万円に対して約0.5%のプラスになっています。
積立時の損益を値動きのグラフに反映させると以下の図のようになります。
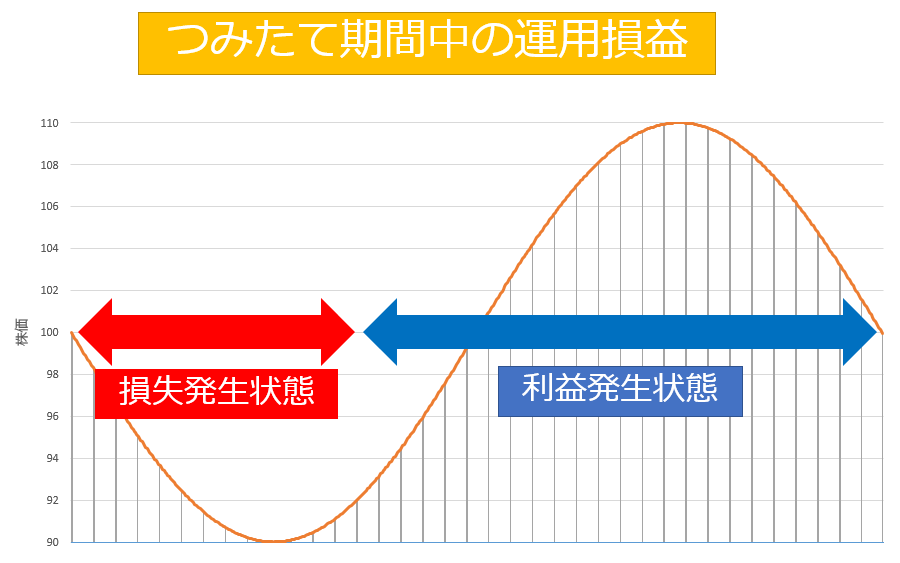
最初の株価沈み局面において、株価が100円まで戻らなくても93円程度の部分から運用状況はプラスになっています。これはつみたてによる大きな効果といえるでしょう。
最終的に元の株価まで下がってしまうとそれほど大きな利益は得られませんが、株価がピークの付近で売ることができれば大きな利益が得られるでしょう。
値動きパターン3:谷
下図のような、コサインカーブとなるような値動きの場合を想定します。
36回のそれぞれの購入時の株価とそれに応じた購入株数などをまとめると以下の表になります。
| 購入 回数 | 株価 | 10,000円で 買える株数 | 投資額 | 評価額 | 損益 |
| 1 | 110.0 | 90.9 | 10,000 | 10,000 | 0 |
| 2 | 109.8 | 91.0 | 20,000 | 19,985 | ▲ 15 |
| 3 | 109.4 | 91.4 | 30,000 | 29,899 | ▲ 101 |
| 4 | 108.6 | 92.1 | 40,000 | 39,688 | ▲ 312 |
| 5 | 107.5 | 93.0 | 50,000 | 49,305 | ▲ 695 |
| 6 | 106.3 | 94.1 | 60,000 | 58,714 | ▲ 1,286 |
| 7 | 104.8 | 95.5 | 70,000 | 67,891 | ▲ 2,109 |
| 8 | 103.1 | 97.0 | 80,000 | 76,827 | ▲ 3,173 |
| 9 | 101.4 | 98.6 | 90,000 | 85,530 | ▲ 4,470 |
| 10 | 99.6 | 100.4 | 100,000 | 94,024 | ▲ 5,976 |
| 11 | 97.8 | 102.2 | 110,000 | 102,350 | ▲ 7,650 |
| 12 | 96.1 | 104.0 | 120,000 | 110,568 | ▲ 9,432 |
| 13 | 94.5 | 105.8 | 130,000 | 118,752 | ▲ 11,248 |
| 14 | 93.1 | 107.4 | 140,000 | 126,987 | ▲ 13,013 |
| 15 | 92.0 | 108.8 | 150,000 | 135,371 | ▲ 14,629 |
| 16 | 91.0 | 109.9 | 160,000 | 144,004 | ▲ 15,996 |
| 17 | 90.4 | 110.6 | 170,000 | 152,989 | ▲ 17,011 |
| 18 | 90.0 | 111.1 | 180,000 | 162,423 | ▲ 17,577 |
| 19 | 90.0 | 111.1 | 190,000 | 172,394 | ▲ 17,606 |
| 20 | 90.3 | 110.7 | 200,000 | 182,973 | ▲ 17,027 |
| 21 | 90.9 | 110.0 | 210,000 | 194,211 | ▲ 15,789 |
| 22 | 91.8 | 108.9 | 220,000 | 206,134 | ▲ 13,866 |
| 23 | 93.0 | 107.5 | 230,000 | 218,739 | ▲ 11,261 |
| 24 | 94.4 | 105.9 | 240,000 | 231,995 | ▲ 8,005 |
| 25 | 96.0 | 104.2 | 250,000 | 245,839 | ▲ 4,161 |
| 26 | 97.6 | 102.4 | 260,000 | 260,176 | 176 |
| 27 | 99.4 | 100.6 | 270,000 | 274,887 | 4,887 |
| 28 | 101.2 | 98.8 | 280,000 | 289,827 | 9,827 |
| 29 | 103.0 | 97.1 | 290,000 | 304,834 | 14,834 |
| 30 | 104.6 | 95.6 | 300,000 | 319,732 | 19,732 |
| 31 | 106.1 | 94.2 | 310,000 | 334,337 | 24,337 |
| 32 | 107.4 | 93.1 | 320,000 | 348,469 | 28,469 |
| 33 | 108.5 | 92.2 | 330,000 | 361,954 | 31,954 |
| 34 | 109.3 | 91.5 | 340,000 | 374,632 | 34,632 |
| 35 | 109.8 | 91.1 | 350,000 | 386,365 | 36,365 |
| 36 | 110.0 | 90.9 | 360,000 | 397,041 | 37,041 |
| 最終値 | 110.0 | 360,000 | 397,047 | 37,047 |
前半の下落局面では損失が投資額の最大10%程度まで拡大していますが、その後の株価回復により最終的には10%程度の利益が生じています。
積立時の損益を値動きのグラフに反映させると以下の図のようになります。
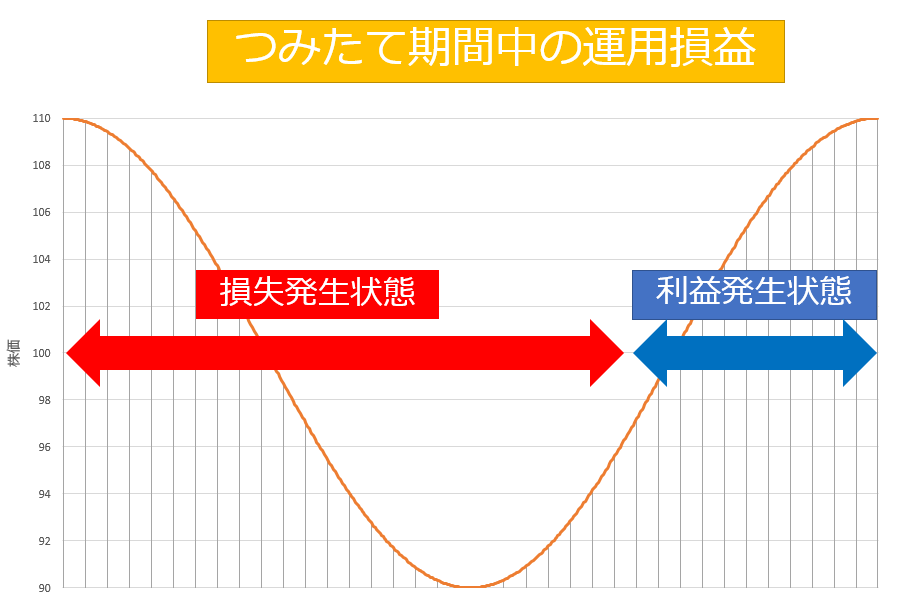
最初に一括で購入した場合、株価が常に最初の値より低いので常に損失が生じている状態となりますが、積立による効果により株価が完全に回復しなくても、約97円の段階で損益はプラスに転換しています。
値動きパターン4:山
下図のような、コサインカーブの逆位相となるような値動きの場合を想定します。
36回のそれぞれの購入時の株価とそれに応じた購入株数などをまとめると以下の表になります。
| 購入 回数 | 株価 | 10,000円で 買える株数 | 投資額 | 評価額 | 損益 |
| 1 | 90.0 | 111.1 | 10,000 | 10,000 | 0 |
| 2 | 90.2 | 110.9 | 20,000 | 20,018 | 18 |
| 3 | 90.6 | 110.3 | 30,000 | 30,123 | 123 |
| 4 | 91.4 | 109.4 | 40,000 | 40,380 | 380 |
| 5 | 92.5 | 108.2 | 50,000 | 50,843 | 843 |
| 6 | 93.7 | 106.7 | 60,000 | 61,552 | 1,552 |
| 7 | 95.2 | 105.0 | 70,000 | 72,530 | 2,530 |
| 8 | 96.9 | 103.2 | 80,000 | 83,780 | 3,780 |
| 9 | 98.6 | 101.4 | 90,000 | 95,286 | 5,286 |
| 10 | 100.4 | 99.6 | 100,000 | 107,011 | 7,011 |
| 11 | 102.2 | 97.9 | 110,000 | 118,900 | 8,900 |
| 12 | 103.9 | 96.3 | 120,000 | 130,882 | 10,882 |
| 13 | 105.5 | 94.8 | 130,000 | 142,872 | 12,872 |
| 14 | 106.9 | 93.6 | 140,000 | 154,775 | 14,775 |
| 15 | 108.0 | 92.6 | 150,000 | 166,492 | 16,492 |
| 16 | 109.0 | 91.8 | 160,000 | 177,923 | 17,923 |
| 17 | 109.6 | 91.2 | 170,000 | 188,970 | 18,970 |
| 18 | 110.0 | 90.9 | 180,000 | 199,546 | 19,546 |
| 19 | 110.0 | 90.9 | 190,000 | 209,576 | 19,576 |
| 20 | 109.7 | 91.2 | 200,000 | 219,000 | 19,000 |
| 21 | 109.1 | 91.7 | 210,000 | 227,779 | 17,779 |
| 22 | 108.2 | 92.5 | 220,000 | 235,899 | 15,899 |
| 23 | 107.0 | 93.5 | 230,000 | 243,366 | 13,366 |
| 24 | 105.6 | 94.7 | 240,000 | 250,217 | 10,217 |
| 25 | 104.0 | 96.1 | 250,000 | 256,512 | 6,512 |
| 26 | 102.4 | 97.7 | 260,000 | 262,338 | 2,338 |
| 27 | 100.6 | 99.4 | 270,000 | 267,807 | ▲ 2,193 |
| 28 | 98.8 | 101.2 | 280,000 | 273,049 | ▲ 6,951 |
| 29 | 97.0 | 103.0 | 290,000 | 278,218 | ▲ 11,782 |
| 30 | 95.4 | 104.8 | 300,000 | 283,476 | ▲ 16,524 |
| 31 | 93.9 | 106.5 | 310,000 | 288,998 | ▲ 21,002 |
| 32 | 92.6 | 108.0 | 320,000 | 294,961 | ▲ 25,039 |
| 33 | 91.5 | 109.3 | 330,000 | 301,539 | ▲ 28,461 |
| 34 | 90.7 | 110.3 | 340,000 | 308,893 | ▲ 31,107 |
| 35 | 90.2 | 110.9 | 350,000 | 317,172 | ▲ 32,828 |
| 36 | 90.0 | 111.1 | 360,000 | 326,496 | ▲ 33,504 |
| 最終値 | 90.0 | 360,000 | 326,490 | ▲ 33,510 |
パターン3と逆で、前半の状況局面では投資額の最大10%程度の利益が発生しているが、最終的には10%弱の損失が発生しています。
つみたて時の損益を値動きのグラフに反映させると以下の図のようになります。
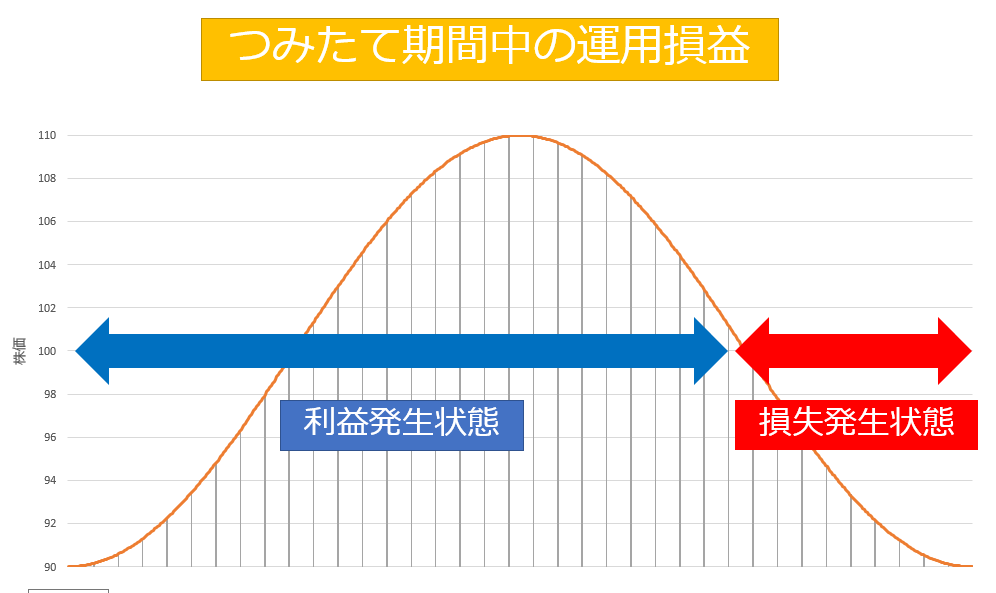
一括購入した場合、常に最初の株価よりも高い値がついているため運用損益はプラスですが、つみたてによって株価が約101円の段階で損益がマイナスになっています。
まとめ
積立投資(時間分散)(ドルコスト平均法)の効果を検証するために三角関数を用いた4つの値動きのパターンについて検証してみました。
最初と最後の株価が同じになるこの4パターンにおいて、最終損益だけに着目すると次のような結果になります。
| 最終損益 | |
| パターン1 | 1,776 |
| パターン2 | 1,760 |
| パターン3 | 37,047 |
| パターン4 | ▲ 33,510 |
この4パターンが等しい確率で起こるとして期待値を考えると、一括購入した場合は損益が0円に対して、積立の場合は+1,768円となります。投資額36万円の割合から考えるとわずか約0.5%であり、計算時の四捨五入等の誤差も含んでいることを考慮するとそれほど大きな差はないと考えられます。以前の記事の結果からも一括購入とつみたての最終結果の比較において、期待値に大きな差は出ないことがわかっています。
積立の場合にとって最も都合の良いシナリオはパターン3のような下落した後に上昇する値動きです。このようなつみたての効果を最大限に活かすためには下落局面で怖がって辞めてしまわないことです。「下落局面こそその後の反発に備えたチャンス」と捉えることが大事になります。下落局面を乗り越えた先は元の株価まで回復しなくても、少しでも回復してくれれば運用損益がプラスになることが今回の図説でご理解いただけたでしょう。
積立の投資を始めるならこちらから↓↓↓